My assumption is that you are trying to find out how old the hide is. I'm going with that. The formula is given to us. Our N value is 30, our
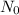
is 100, and we are given the constant k as -.0001. Setting up our formula accordingly, we have

. In solving for t, we are left with the problem of getting out from the exponent that it's in to down on a level where we can deal with it. Natural logs and Euler's number "undo" each other, if you will, just to "undo" a square root we would square it. We will take the natural log of both sides to "undo" Euler's number. (It actually is because natural logs have a base of "e", but nonetheless...). First things first, we will divide both sides by 100 to get

and then take the natural log of both sides.
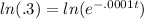
. But like I said, taking the natural log of the right side undoes Euler's number, so what the rule allows us to do is eliminate the ln and e:
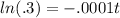
. The natural log of a decimal will always be a negative number, -1.203972 to be exact.
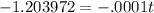
. We divide both sides by -.0001 to solve for t. We find that the hide, then, is 12,039 years old.