The correct answers for x would be
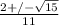
.
In order to find this, we must first get the equation to equal 0. In order to do that, subtract 1 from each side to get the following.
11

- 4x - 1 = 0
Knowing this we can now use the quadratic equation using a = 11, b = -4 and c = -1. The quadratic equation is below.
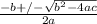
Now we can plug the values into the equation to solve.
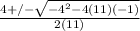
Then simplify using the order of operations.
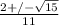
.