Between the probability of union and intersection, it's not clear what you're supposed to compute. (I would guess it's the probability of union.) But we do know that
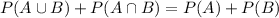
For parts (a) and (b), you're given everything you need to determine
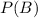
.
For part (c), if
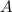
and
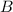
are mutually exclusive, then
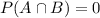
, so
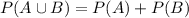
. If the given probability is
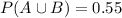
, then you can find
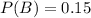
. But if this given probability is for the intersection, finding
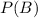
is impossible.
For part (d), if
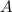
and
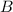
are independent, then
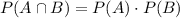
.