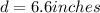Question

For a party, three solid cheese balls with diameters of 2 inches, 4 inches, and 6 inches, respectively, were combined to form a single cheese ball. what was the approximate diameter, in inches, of the new cheese ball? (the volume of a sphere is 43πr3,

Answer 1

The first thing we must do for this case is to define the volume of a sphere.
We have then:

`V = (4)/(3) * (\pi) * (r ^ 3)`
Where,
r: sphere radio
We look for the total volume of cheese balls.
We have then:

`Vt = (4)/(3) * (\pi) * (( (2)/(2) ) ^ 3 + ((4)/(2))^3 + ((6)/(2))^3)`

`Vt = (4/3) * (\pi) * ((1) ^ 3 + (2) ^ 3 + (3) ^ 3) Vt = (4/3) * (\pi) * (1 + 8 + 27) Vt = 48 (\pi)`
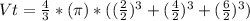
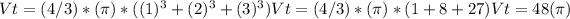
Then, Rewriting the left side of the equation we have:

`(4)/(3) * (\pi) * (r ^ 3) = 48 (\pi)`
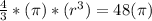
Clearing the radio we have:

`r ^ 3 = (3)/(4) * (48)`

`r ^ 3 = 36`

`r = (36) ^ {(1/3)}`

`r = 3.3 inches`
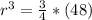
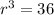
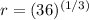
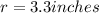
Then, the diameter will be:

`d = 2 * 3.3 d = 6.6 inches`
Answer:
The approximate diameter, in inches, of the new cheese ball is:

`d = 6.6 inches`