Answer:
The correct option is D.
Explanation:
If function f(x) is called an even function if f(-x)=f(x).
The first function is
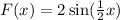
Put x=-x,
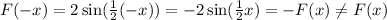
![[\because \sin(-x)=-\sin x]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/ai1lpggtips8fhwff20ylid2aqmter0por.png)
So, this function is not an even function.
The second function is
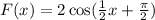
Put x=-x,
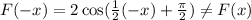
So, this function is not an even function.
The third function is
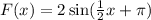
Put x=-x,
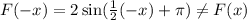
So, this function is not an even function.
The fourth function is
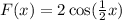
Put x=-x,
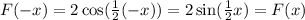
![[\because \cos(-x)=\cos x]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/vf9y1oiki4qdwns9957az9lcv87t52zuen.png)
So, this function is an even function.
Hence the correct option is D.