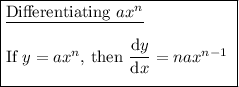Answer:
(0, 21)
Explanation:
Stationary points occur when the gradient of a graph is zero.
Therefore, to find the x-coordinate(s) of the stationary points of a function, differentiate the function, set it to zero and solve for x.
Differentiate the given function:
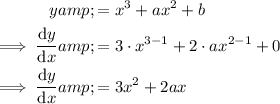
Set the differentiated function to zero:
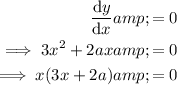
Therefore the stationary points occur when:
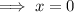
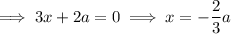
There is a stationary point at (4, -11), therefore substitute x = 4 into the expression for x and solve for a:
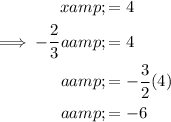
Substitute the found value of a and the point (4, -11) into the function and solve for b:
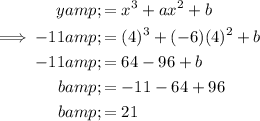
Therefore, the function is:
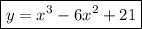
The other stationary point is when x = 0. Therefore, to find the coordinates of this point, substitute x = 0 into the function:
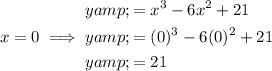
Therefore, the coordinates of the other stationary point are (0, 21).
To determine if a stationary point is minimum or maximum, differentiate the function again:
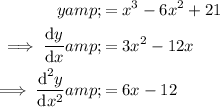
Substitute the x-coordinate of the stationary point into the second derivative:


Differentiation Rules