Question

Which counterexample disproves the conjecture?

A student concludes that if x is a real number, then x ≥ x^3.

A. x= 3
B. x= 1
C. x= 0
D. x= -1

Answer 1

If one were to look at the answers, one could try them all out to see which one disproved the conjecture. Starting with a, we get that 3 is => 27. Since this is obviously not true, we know that the correct answer is A. 

Answer 2

Let's check all x for satisfiyng the inequality
`x\ge x^3`:
1. x=3, then the inequality
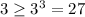
`3\ge 3^3=27` is false;
2. x=1, then the inequality
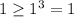
`1\ge 1^3=1` is true;
3. x=0, then the inequality
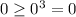
`0\ge 0^3=0` is true;
4. x=-1, then the inequality
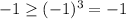
`-1\ge (-1)^3=-1` is true.

Answer: counterexample A disproves the conjecture.