Question

A)38.5 units

B)42.0 units

C)33.2 units

D)32.8 units

Answer 1

33.2 is correct just took the test.

Answer 2

You have to use the distance formula for lengths of XZ, ZY, and YX. Filling in the formula for the distance that they provided,
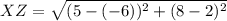
`XZ= √((5-(-6))^2+(8-2)^2)` and
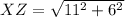
`XZ= √(11^2+6^2)` which is
`XZ= √(157)` which, in decimal form is 12.5299. Now onto the next length, ZY:
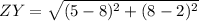
`ZY= √((5-8)^2+(8-2)^2)` and
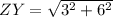
`ZY= √(3^2+6^2)` which is
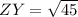
`ZY= √(45)` which, in decimal form is 6.70820. Now onto the last segment, YX:
`YX= √((8-(-6))^2+(2-2)^2)` and
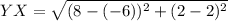
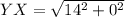
`YX= √(14^2+0^2)` and of course the square root of 14 squared is 14. So our sides lengths are, for the perimeter, 12.5299+6.70820+14=33.2 units.