Answer:
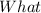
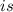
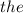

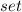
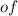
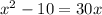


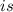
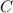
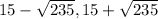
What is the solution set of
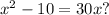 ?
?
A) {–220, 250}
B) {–250, 220}
✔ C)
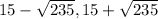
D)

Explanation:
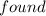

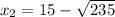



Step-by-step solution
Solving quadratic equations by completing the square
1. Move all terms to the left side of the equation
2. Find the coefficients
To find the coefficients, use the standard form of a quadratic equation:
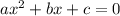
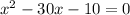
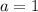
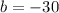
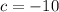
3. Move the constant to the right side of the equation and combine
Add -10 to both sides of the equation:
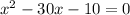
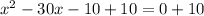
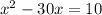
4. Complete the square
To make the left side of the equation into a perfect square trinomial, add a new
constant equal to
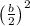 to the equation:
to the equation:
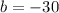
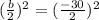
Use the exponents fraction rule
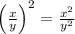

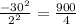
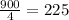
Add 225 to both sides of the equation:
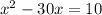
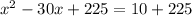
Simplify the arithmetic:
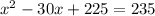
Now we have perfect square trinomial, we can write it as a perfect square form by
adding half of the
 coefficient,
coefficient,
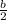 :
:
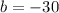
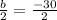
2 additional steps
Find the greatest common factor of the numerator and denominator:
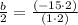
Factor out and cancel the greatest common factor:
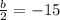
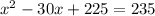
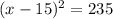
5. Solve for

Take the square root of both sides of the equation: IMPORTANT: When finding the
square root of a constant, we get two solutions: positive and negative
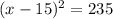
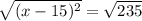
Cancel out the square and square root on the left side of the equation:
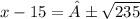
Add
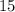 to both sides
to both sides
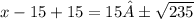
Simplify the left side:
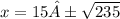

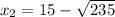


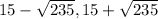 .
.
Have a Nice Day .