Question

the tip of a pinwheel is 0.24 m from the center. The pinwheel spins 5 times each second. What is the tangential speed of the tip of the pinwheel?

Answer 1

D. 7.5

Step-by-step explanation:

edge2020

Answer 2

Answer: 7.539 m/s

Step-by-step explanation:

The tangential velocity
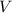`V` is defined as the angular velocity
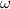`\omega` by the radius
`r` of the circular motion:

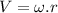`V=\omega. r` (1)

Its name is due to the fact that this linear velocity vector is always tangent to the trajectory and is the distance traveled by a body or object in a circular movement in a period of time.

In this sense,
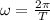`\omega=(2 \pi)/(T)` is the angular velocity, which is inversely proportional to the period
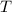`T` of the circular motion. So equation (1) is expressed as:

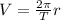`V=(2 \pi)/(T)r` (2)

We already know
`r=0.24 m` , and we can find
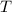`T`, knowing the frequency
`f`:

`f=5 times/s=(1)/(T)`

Isolating
`T`:

`T=(1)/(f)=(1)/(5 times/s)`

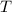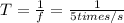
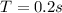`T=0.2 s` (3)

Substituting (3) in (2):

`V=(2 \pi)/(0.2 s)(0.24 m)` (4)

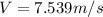`V=7.539 m/s` This is the tangential speed of the tip of the pinwheel