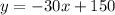Question

PLEASE HELP: 25 pts Ivy has borrowed 150 songs from her friend. She plans to download an equal number of songs on her music player each week for 5 weeks.

The graph shows the number of songs left to download, y, for a certain number of weeks, x: A graph titled Song Downloading shows Number of Weeks on x-axis and Number of Songs Left to Download on y-axis.

The x-axis scale is shown from 0 to 5 at increments of 1, and the y-axis scale is shown from 0 to 210 at increments of 30. A straight line joins the ordered pairs 0, 150 and 1, 120 and 2, 90 and 3, 60 and 4, 30 and 5, 0.

Part A: What is the rate of change and initial value of the function represented by the graph, and what do they represent in this scenario? Show your work to find the rate of change and initial value.

Part B: Write an equation in slope-intercept form to model the relationship between x and y.

Answer 1

Answer: y=-30x+150

Step-by-step explanation:So 150/5=30 which are the number of weeks and the total number of songs.

Since every week she downloads 5 songs this makes the total quantity which makes it go less makes the 30 a negative number.

Initial number is 150 since its the total of songs that are in total.

M=(120-150)/(1-0)=-30

Line equation

y=150=-30(x-0)

y=-30x+150

Answer 2

Part A:

For this case, the rate of change is given by the slope of the straight line.
We have then:

`m= (y2-y1)/(x2-x1)`
Substituting values we have:

`m= (0-150)/(5-0)`
Rewriting:

`m= (-150)/(5)`

`m=-30`
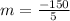
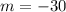
On the other hand, the initial value of the function occurs when x = 0.
We then have that for x = 0 the value of the function is 150.
Therefore we have:

`b = 150`
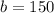Answer:
m=-30, b = 150
The slope of the line represents the number of songs downloaded per week.
The cut-off point with the y-axis represents the initial number of songs that must be downloaded

Part B:

For this case the generic equation of the line is given by:

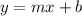
`y = mx + b` Where,
m: slope of the line
b: cutting point with the y axis.
Substituting the values of the part we have:

`y=-30x+150`
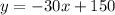Answer:
An equation in slope-intercept form to model the relationship between x and y is:

`y=-30x+150`