Question

Consider the function g(x)=2x^3+7x^2+x-10-5/2 is a root of g(x). Find all of the roots of g(x)

Answer 1

If -5/2 is a root of that 3rd degree polynomial, then when we do synthetic division on it we will get a remainder of 0, and the resulting numbers from our math will then become the coefficients to a new polynomial, one degree less than what we started with, called the depressed polynomial. Put -5/2 outside the "box" and the coefficients inside: -5/2 (2 7 1 -10). Bring down the 2 and multiply it by -5/2 to get -5. Put that -5 up under the 7 and add to get 2. Multiply that 2 by the -5/2 to get -5. Put that -5 up under the 1 and add to get -4. Multiply that by -5/2 and get 10. Put that 10 up under the -10 and add to get a remainder of 0. Those bolded numbers now are the coefficients of our new polynomial, one degree less than what we started with. That polynomial is
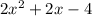
`2x^2+2x-4`. Now we need to factor that to find the other 2 roots to our polynomial. If we factor a 2 out we have
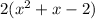
`2( x^(2) +x-2)`,That factors easily to 2(x+2)(x-1). That gives us x+2=0 and x = -2, x-1=0 and x = 1. The 3 solutions or zeros or roots are -5/2, -2, 1. There you go!