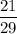Question

Find the cosine of angle P.
A.20/29
B.21/29
C.20/21
D.21/20

Answer 1

20/29 is the cosine because it’s adjacent over hypotenuse

Answer 2

`\cos P=(21)/(29)`

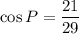
B is correct

Explanation:

In the given figure, we need to find cosine of P

In ΔPRQ, ∠R=90°. So, triangle PRQ is a right angle triangle. We can apply trigonometry identity.

As we know,

`\cos\theta=\frac{\text{Base}}{\text{Hypotenuse}}`

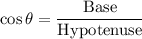
In given triangle, For angle, ∠P

Base = 21

Hypotenuse = 29

Substitute into formula and we get

`\cos P=(21)/(29)`

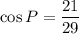
Hence, The cosine of P is
`(21)/(29)`