If you plot these points on a piece of graph paper, you will see that the point (-2,7) is directly above the point (-2,1) because they share the same x value. They both fall on a perfectly vertical line. If they both fall on a perfectly vertical line, all you have to do to find the length of that segment is to count the number of units 1 is above the other. That's 6. The same goes for the points (4,7) and (4,1). They are also on the same perfectly vertical line so they are also 6 units apart and the length of that segment is 6. Btw, this polygon looks like a house that a kid would draw with a pointy roof. The side lengths I just gave you were the sides of the house. In order to find the length of the base of the house, we count the x units between the 2 points (-2,1) and (4,1). The distance between -2 and 4 is 6. So far we have 3 measurements for this house, and all 3 are 6. Now we come to the pointy roof on the house. It's a line that is a diagonal, so we will use the distance formula here to get the correct measure. The distance formula is
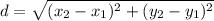
. Filling in using the endpoints for that segment we have
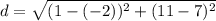
. That simplifies to
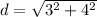
which simplifies even further to
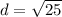
and d = 5. The other slant now...
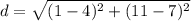
which simplifies to
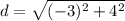
which simplifies further to
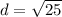
and d = 5. So the side lengths for our polygon are 6+6+6+5+5 which equals 28 units. There you go!