Question

The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 30 inches, and the girth of 20 inches (perimeter of the side formed by the width and height), what is its height? Use k = 24. (Hint: Volume = length width height. Solve for length, and substitute into the equation for constant of proportionality.) ___ inches or ___ inches

Answer 1

V = kl where k is the constant of proportionality

V = 24l = 24*30 = 720 in^3

720 = 30*h*w
hw = 720 / 30 = 24
also 2h + 2w = 20
w + h = 10
24/h + h = 10
24 + h^2 = 10h
h^2 - 10h + 24 = 0
(h - 4)(h - 6)=0

h = 4 inches or 6 inches.

Answer 2

Volume of box (V) is given by:

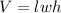`V = lwh` .....[1]

where,

l is the length , w is the width and h is the height of the box respectively.

As per the statement:

The volume of a box(V) varies directly with its length(l).

`V \propto l`

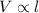
then;

`V = kl` where, k is the constant of proportionality.

Substitute k = 24 and l = 30 inches we have;

`V = 24 \cdot 30 = 720 in^3`

Substitute the given values of V and l in [1] we have;

`720 = 30wh`

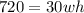
Divide both sides by 30h we have;

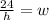`(24)/(h) =w` .....[2]

It is also given that the girth of 20 inches (perimeter of the side formed by the width and height)

Perimeter of rectangle formed by width and height is given by:

P = 2(w+h)

then;

`20 = 2(w+h)`

Divide both sides by 2 we have;

`10 = w+h`

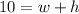
or

w+h = 10 .....[3]

Substitute equation [2] into [3] we have;

`(24)/(h)+h = 10`

⇒
`24 +h^2 = 10h`

⇒
`h^2-10h+24 = 0`

⇒
`h^2-6h-4h+24=0`

⇒
`h(h-6)-4(h-6)=0`

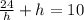
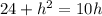
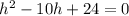
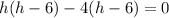
Take h-6 common we have;

⇒
`(h-6)(h-4)=0`

By zero product property we have;

h-6=0 or h-4=0

⇒h = 6 inches or h = 4 inches.

therefore, the height is, 6 or 4 inches