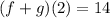Question

If f(x) = 2x2 + 3x and g(x) = x – 2, what is (f + g)(2)?

Answer 1

For this case we have the following functions:

`f(x) = 2x^2 + 3x g(x) = x - 2`
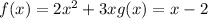
The first thing we must do is calculate the sum of functions or equivalently:

`(f + g)(x) = f(x) + g(x)`
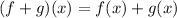
We have then:

`(f + g)(x) = (2x^2 + 3x) + (x - 2)`
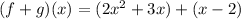
To complete the sum, we must add the terms whose exponents are equal.
We have then:

`(f + g)(x) = 2x^2 + (3x + x) - 2 (f + g)(x) = 2x^2 + 4x - 2`
Then, we evaluate the function for x = 2:

`(f + g)(2) = 2(2)^2 + 4(2) - 2`
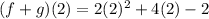
Rewriting we have:

`(f + g)(2) = 2(4) + 4(2) - 2 (f + g)(2) = 8 + 8 - 2 (f + g)(2) = 14`
Answer:

`(f + g)(2) = 14`