Question

Which is the graph of f(x) = 3 (3/2)^x ?

Answer 1

The answer will be D.

Answer 2

The graph of the function f(x) is:

Graph 4

Explanation:

We are given a function f(x) in terms of variable x as follows:

`f(x)=3\cdot ((2)/(3))^x`

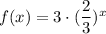
Now, when x=0 then the graph of the function f(x) must pass through:

`f(x)=3\cdot ((2)/(3))^0\\\\i.e.\\\\f(x)=3`

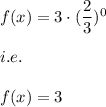
and when x=1 then the graph of the function f(x) must pass through:

`f(x)=3\cdot ((2)/(3))^1\\\\i.e.\\\\f(x)=2`

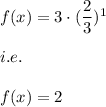
i.e. the graph of the function should pass through the points:

(0,3) and (1,2)

Now, after looking at the graph we observe that the first and second graph do not pass through (0,3).

Hence, graph 1 and graph 2 do not represent the function f(x).

Also, graph 3 pass through (0,3) but it does not pass through (1,2)

Hence, Graph 3 does not represent f(x)

Hence, the correct graph is: Graph 4