Final answer:
The estimated population after 5 years is approximately 413 animals.
Step-by-step explanation:
To model the situation, we can use the formula for exponential growth:
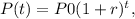 where P(t) is the population after t years, P0 is the initial population, r is the annual growth rate, and t is the number of years.
where P(t) is the population after t years, P0 is the initial population, r is the annual growth rate, and t is the number of years.
In this case, the initial population is 290 animals and the annual growth rate is 9%, which can be expressed as 0.09.
The function becomes:
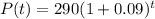 .
.
To estimate the value of the function after 5 years, we substitute t = 5 into the formula and calculate:
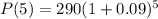
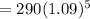
= 413.
Therefore, the estimated population after 5 years is approximately 413 animals.