Answer:
B. 63°.
Explanation:
Please find the attachment.
Let x be the measure of each base angle of the isosceles trapezoid.
We have been given that the isosceles trapezoid is part of an isosceles triangle with a 54° vertex angle. We are asked to find the measure of an acute base angle of the trapezoid.
Upon looking at our attachment we can see that measure of base angle of trapezoid will be equal to the measure of base angle of isosceles triangle.
To find the base angle of trapezoid we will use angle sum property. Since both angles of an isosceles triangle are equal, so we can set an equation as:
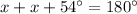
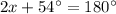
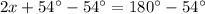
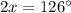
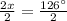
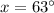
Therefore, the measure of an acute base angle of the trapezoid is 63 degrees and option B is the correct choice.