Answer:
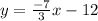
Explanation:
Point-slope form is
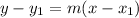 . The
. The
 ,
,
 , and
, and
 have to be substituted for with real values in order to make an equation of a line. From there, you can isolate
have to be substituted for with real values in order to make an equation of a line. From there, you can isolate
 to turn it into slope-intercept form.
to turn it into slope-intercept form.
1) First, let's find the slope of the line, which is represented by the variable
 . Use the slope formula,
. Use the slope formula,
 , to find the slope.
, to find the slope.
 and
and
 are the x and y values of one point,
are the x and y values of one point,
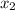 and
and
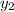 are the x and y values of another point. For this problem, let's use the given points (-3, -5) and (-6, 2):
are the x and y values of another point. For this problem, let's use the given points (-3, -5) and (-6, 2):
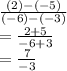
Thus, the slope is
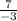 .
.
2) Now that we have the slope, let's substitute it into the point-slope formula. The
 and
and
 represent the x and y values of a point that the line intersects so you could either use (-3, -5) or (-6,2), but for this answer, I used (-6,2). (The answer will always be the same no matter which point you choose.) Substitute these values then isolate y to put it in slope-intercept form:
represent the x and y values of a point that the line intersects so you could either use (-3, -5) or (-6,2), but for this answer, I used (-6,2). (The answer will always be the same no matter which point you choose.) Substitute these values then isolate y to put it in slope-intercept form:
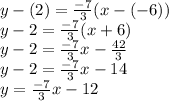
So,
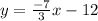 is the answer.
is the answer.