Question

∆ABC has the points A(1, 7), B(-2, 2), and C(4, 2) as its vertices.The measure of the longest side of ∆ABC isa)5b)6c)29^(1/2)

d.34^(1/2)units. ∆ABC is triangle.
a.equilateralb)isosceles
c.rightd)scaleneIf ∆ABD is formed with the point D(1, 2) as its third vertex, then ∆ABD is trianglea)equilateralb)isosceles
c.rightd)scaleneThe length of side AD is
a.3
b.5
c.8
d.10 units.

Answer 1

the other guy is right the only thing is that the right triangle is a right scalene

Explanation:

Answer 2

• The measure of the longest side of ∆ABC is:

b) 6

• ∆ABC is :

b) isosceles triangle.

• ∆ABD is :

c) right triangle

• The length of side AD is :

b) 5

Explanation:

• The vertices of ∆ABC are:

A(1, 7), B(-2, 2), and C(4, 2)

Length of AB is:

`AB=√((-2-1)^2+(2-7)^2)\\\\\\AB=√(3^2+5^2)\\\\\\AB=√(9+25)\\\\\\AB=√(34)\ units`

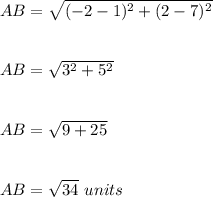
Length of BC is:

`BC=√((4-(-2))^2+(2-2)^2)\\\\\\BC=√(6^2)\\\\\\BC=6\ units`

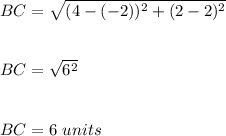
Length of AC is:

`AC=√((4-1)^2+(2-7)^2)\\\\\\AC=√(3^2+5^2)\\\\\\AC=√(34)\ units`

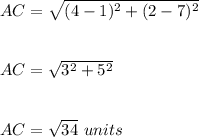
Since, the length of side AC=length of side AB.

Hence, we get:

The triangle is a isosceles triangle.

Also, the longest side of a triangle is: 6 units.

• Now, when a new vertex D(1,2) is added.

then:

Length of AD=

`AD=√((1-1)^2+(2-7)^2)\\\\\\AD=√(5^2)\\\\\\AD=5\ units`

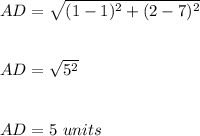
Length BD

`BD=√((1-(-2))^2+(2-2)^2)\\\\\\BD=√(3^2)\\\\\\BD=3\ units`

and Length AB is:
`√(34)\ units`

Also, AD,BD and AB satisfy the Pythagorean Theorem.

Since,

`AB^2=√(AD^2+BD^2)`

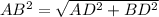
Hence,

∆ABD is a right angled triangle.

and the length of side AD is 5 units