Question

Find all relative extrema of the function. use the second derivative test where applicable. (if an answer does not exist, enter dne.) f(x) = x3 − 9x2 + 2

Answer 1

First find the derivative of the function. The derivative is
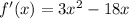
`f'(x)=3 x^(2) -18x`. Now set it equal to 0 to find the critical numbers.
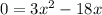
`0=3 x^(2) -18x`. Factor to solve for the zeros of the derivative.
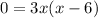
`0=3x(x-6)`. So 3x = 0, and x = 0, or x - 6 = 0 and x = 6. We will make a table with values for -∞<x<0, 0<x<6, 6<x<∞. Pick a value within those boundaries for each interval and find the sign, positive or negative, that results from subbing that number into the derivative. If we choose -1 in the first interval f'(-1)=21, so the function is increasing from negative infinity to 0. If we choose 1 in the second interval, f'(1)=-15, so the function is decreasing from 0 to 6. If we choose 10 in the last interval, f'(10)=120, so the function is increasing from 6 to infinity. The points of extrema are found by subbing the critical x values into the original function. We know the function is increasing from negative infinity to 0, so f(0)=2, and our max point is (0, 2). We know the function is decreasing from 6 to infinity, so f(6)=-106, and our min point is (6, -106). I do this instead of the second derivative test, but they both work.