Question

Suppose that f(x)=x^2 and g(x)=4x^2-2. which statement best compares the graph of g(x) with the graph of f(x)?

a. the graph of g(x) is the graph of f(x)compressed vertically and shifted 2 units to the right.
b. the graph of g(x) is the graph of f(x)compressed vertically and shifted 2 units down.
c. the graph of g(x) is the graph of f(x)stretched vertically and shifted 2 units down.
d. the graph of g(x) is the graph of f(x)stretched vertically and shifted 2 units to the right????? HELP ASAP

Answer 1

The standard form of a parabola is
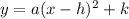
`y=a(x-h)^2+k`, where h and k are the coordinates of the vertex and the a is the value that either compresses it vertically or draws it out horizontally (aka stretched). The h value also indicates side to side movement, while the k value indicates up or down movement. The larger the a value, the closer the parabola "hugs" the axis of symmetry. All in all here, we have a parabola in g(x) that is vertically compressed and is moving down from its original vertex of f(x) which (0, 0) by 2 units. Therefore, our choice is b.

Answer 2

The graph of G(x) is the graph of F(x) stretched vertically and shifted 2 units down.

Explanation: