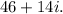Answer: The required standard form of the product is
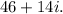
Step-by-step explanation: We are given to find the product of the following two complex numbers and write the answer is standard complex number form.
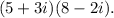
We know that
a complex number z can be written in standard complex number form as follows :
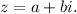
Now,
![(5+3i)(8-2i)\\\\=5*8-5*2i+3i*8-3i*2i\\\\=40-10i+24i-6i^2\\\\=40+14i+6~~~~~~~~~~~[\textup{since }i^2=-1]\\\\=46+14i.](https://img.qammunity.org/2019/formulas/mathematics/high-school/q4rhhq11q2bawas3y74qi7hwgybc6xgn1k.png)
Thus, the required standard form of the product is