If we plot that point we find ourselves in QIV. The distance along the x axis is 4, and the distance down from that point is -3. If we create a right triangle with that segment, that segment serves as the hypotenuse of the triangle. We need its measure. Using Pythagorean's theorem,
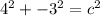
and
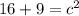
. We see that c = 5. We need now to find the secant of that right triangle. Secant if the co-identity of cosine which is side adjacent over hypotenuse. That means that secant is the hypotenuse over the side adjacent. So our secant theta = 5/4