13x + 2y = 1
5x - 2y = -19
Use the substitution method to solve this system of equations. In the first equation, solve for y.
13x + 2y = 1
Subtract 13x from both sides.
2y = 1 - 13x
Divide both sides by 2.
y =

-
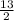
x
Now plug y into the second equation.
5x - 2(

-
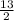
x) = -19
Distribute -2 to

-
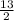
x.
5x - 1 + 13x = -19
Combine like terms.
18x - 1 = -19
Add 1 to both sides.
18x = -18
Divide both sides by 18.
x = -1
Now plug x back into the "new" first equation (where we solved for y).
y =

-
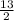
(-1)
Multiply
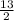
by -1.
y =

+ 6

= 7
y = 7
x = -1, y = 7