Question

What number produces an irrational when added to 1/3

Answer 1

any irrational number (e.g., pie, sqaure2, sqaure3, ect.)

Answer 2

An irrational number produces an irrational when added to
`(1)/(3)`

Explanation:

To find : What number produces an irrational when added to
`(1)/(3)` ?

Solution :

We know that,

`(1)/(3)=0.333....`

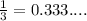
It is a rational number as it is repeating.

So, If we add a rational number into a rational number it always gives you a rational number.

To produce an irrational number,

If we add an irrational number to a rational number it always gives you an irrational number.

For example :

An irrational number -
`\pi`

A rational number -
`(1)/(3)`

Adding these two number,

`\pi+(1)/(3)=3.47492598692...`

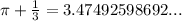
This number is non-terminating and non-repeating.

Therefore, An irrational number produces an irrational when added to
`(1)/(3)`