Question

What is the measure angle AXC

Answer 1

m<AXC = 70

Explanation:

Answer 2

When two chords (straight line with endpoints on the circle) intersect in a circle, like you see in the picture with lines AB and CD, it creates 4 angles. One of the angle AXC, the angle we're trying to find.

If you know the length of the arc that is created by angle AXC (arc AC) and the length of the arc opposite of it (arc DB) you can find the angle of AXC. See picture for the general formulas. The formula for the angle of AXC is:

`m\angle AXC = (1)/(2) (m \overset{\frown}{AC} + m \overset{\frown}{DB})`

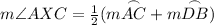
Knowing
`m \overset{\frown}{AC} = 40\°` and
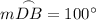
`m \overset{\frown}{DB} = 100\°`, you can plug these values in and solve for
`m\angle AXC`:

`m\angle AXC = (1)/(2) (m \overset{\frown}{AC} + m \overset{\frown}{DB})\\ m\angle AXC = (1)/(2)(40\° + 100\°)\\ m\angle AXC = (1)/(2)(140\°)\\ m\angle AXC = 70\°`

--------

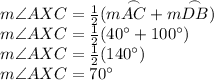
Answer:
`m\angle AXC = 70\°`