Question

A force of 60 N is used to stretch two springs that are initially the same length. Spring A has a spring constant of 4 N/m, and spring B has a spring constant of 5 N/m.

How do the lengths of the springs compare?

How do the lengths of the springs compare?

A.Spring B is 1 m longer than spring A because 5 – 4 = 1.
B.Spring A is the same length as spring B because 60 – 60 = 0.
C.Spring B is 60 m longer than spring A because 300 – 240 = 60.
D.Spring A is 3 m longer than spring B because 15 – 12 = 3.

I don't need the answer the correct answer is D

Answer 1

D on ED

Step-by-step explanation:

Answer 2

We can calculate the length of each spring by using the relationship:

`F=kx`
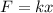
where
F is the force applied to the spring
k is the spring constant
x is the length of the spring (measured with respect to its rest position)

Re-arranging the equation, we have

`x= (F)/(k)`

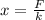
The force applied to both spring is F=60 N. Spring A has spring constant of k=4 N/m, therefore its length with respect to its rest position is

`x_A= (F)/(k_A)= (60 N)/(4 N/m)=15 m`
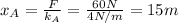
Spring B has spring constant of k=5 N/m, so its length with respect to its rest position is

`x_B= (F)/(k)= (60 N)/(5 N/m)=12 m`

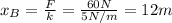
Therefore, the correct answer is
D.Spring A is 3 m longer than spring B because 15 – 12 = 3.