Question

How does the graph of y=-(2x+6)^2+3 compare to the graph of the parent function

A. The graph is compressed horizontally by a factor of 2, shifted left 3, reflected over the x-axis, and translated up 3.
B. The graph is reflected over the x-axis, compressed horizontally by a factor of 2, shifted left 6, and translated up 3.
C. The graph is stretched horizontally by a factor of 2, reflected over the x-axis, shifted left 3, and translated up 3.
D. The graph is reflected over the x-axis, stretched horizontally by a factor of 2, shifted left 6, and translated up 3.

Answer 1

That would be option A .  Note its shifted left 3 not 6   because we have 2x in the parentheses  ( 2x + 6)  = 2(x + 3)

Answer 2

A. The graph is compressed horizontally by a factor of 2, shifted left 3, reflected over the x-axis, and translated up 3.

Step-by-step explanation:

We have been given graph of a function
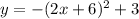`y=-(2x+6)^2+3`. We are asked to compare the graph to the parent function.

Let us recall transformation rules:

Reflection:

`f(x)=-f(x)\Rightarrow\text{Graph reflected about x-axis}`,

`f(x)=f(-x)\Rightarrow\text{Graph reflected about y-axis}`

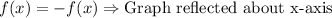Upon looking at our given function, we can see that graph is reflected about x-axis.

Translation:

`f(x-a)\Rightarrow\text{Graph shifted to right by a units}`,

`f(x+a)\Rightarrow\text{Graph shifted to left by a units}`,

`f(x)-a\Rightarrow\text{Graph shifted downwards by a units}`,

`f(x)+a\Rightarrow\text{Graph shifted upwards by a units}`.

`y=-(2(x+3))^2+3`

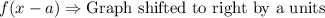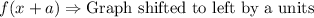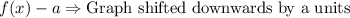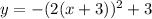
Stretch:

`f(x)=f(ax);a>1\Rightarrow\text{Function compressed horizontally}`

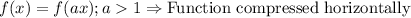
We can see that graph is shifted to left 3 units and upwards by 3 units.

Therefore, option A is the correct choice.