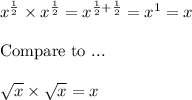Question

Explain why the square root of a number is defined to be
equal to that number to the 1/2 power

Answer 1

9514 1404 393

Answer:

(x^(1/2))^2 = x^(2/2) = x

Explanation:

The square root of a number, when multiplied by itself, gives the original number.

(√x)(√x) = x

The rule for exponents is that powers of the same base, when multiplied, will be the base to the sum of those powers.

(a^b)(a^c) = a^(b+c)

Also, the first power of a number is that number itself.

__

`x^{(1)/(2)}* x^{(1)/(2)}=x^{(1)/(2)+(1)/(2)}=x^1=x\\\\ \text{Compare to ...}\\\\ √(x)*√(x)=x`

Answer 2

Squaring and square root are inverses, so one should "undo" the other. That is, squaring the square root of a number results in the number. Using the power of a power rule, you multiply the exponents. Since a number to the first power is itself, the product of the exponents must equal 1. This means that the power of the square root must be the reciprocal of 2, or one half.

Explanation:

EDGE 2020-2021