Answer:
The equation of the circle is
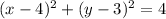 .
.
Explanation:
The radius of required circle is 2 units. The standard equation of a circle is
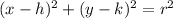 .... (1)
.... (1)
where (h,k) is center of the circle and r is radius.
The given equation of a circle is
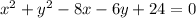

If we have the expression
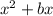 , then we have to add
, then we have to add
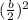 to make the expression a perfect square.
to make the expression a perfect square.
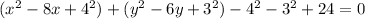
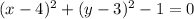
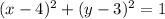 .... (2)
.... (2)
From (1) and (2), we get
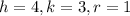
It means the center of this circle is (4,3). So, the center of required circle is also (4,3).
The center is (4,3) and radius is 2, therefore the required equation is
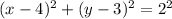
It can also written as
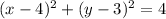
Therefore the equation of the circle is
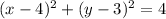 .
.