Question

3. Given the function f(x)=x^2+4x-12:
a. Identify the zeros using factorization.

Answer 1

x = -6, 2

Explanation:

A zero is the x-value of a point on the x-axis that the graph intersects. Knowing this, we can set the function itself to 0 to find the zeros.

1) Set the function to 0.

`x^2+4x-12 = 0`

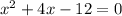
2) Factor out the polynomial. Ask yourself, what are two numbers that have a product of -12 and add up to 4? (In this case, it's 6 and -2.)

`x^2+4x-12 = 0\\(x+6)(x-2) = 0`

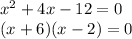
3) Look at the answer from the last step. What do the x's have to equal in order for equation to equal 0? They have to be -6 and 2. Therefore, those are the zeros.