Question

Suppose a  is directly proportional to b, but inversely proportional to c. If a=2 when b=5  and c=9, then what c is when b=3 ?

Answer 1

The given relation means
a = k·b/c
Filling in the given information, you have
2 = k·5/9
k = 18/5 = 3.6

Then for a different value of b with the same value of a, we can find c.
2 = 3.6·3/c
c = 3.6·3/2
c = 5.4

Answer 2

We will have 2 different equations that we will combine into 1, but we need to find the 2 k values first. If a is directly proportional to b, then a = kb. When a = 2 and b = 5, then k = 2/5. Store that for a minute. Now onto the second equation to find the other k value. If a is inversely proportional to c, then a=k/c. If a = 2 when c = 9, then k = 18. We will now use the transitive property: if a=kb and a = k/c, then kb=k/c. The k on the left is 2/5 and we are told that b = 3; the k on the right is 18 and we are looking for c. So here is what we have:
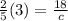
`(2)/(5) (3)= (18)/(c)` and
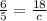
`(6)/(5) = (18)/(c)`. Cross multiply to get 6c = 90 and c = 15.