Question

When the solutions are going to be complex, which methods can be used to solve quadratic equations?

Answer 1

You could complete the square to state the vertex.
You could use the quadratic equation to find the roots (which are complex).

Try an example that will require both.

y = x^2 + 2x + 5

Step One
Get the graph. That's included below.

Step Two
Provide the steps for completing the square.
Note: we should get (-1,4)

y= (x^2 +2x ) + 5
y = (x^2 +2x + 1) + 5 - 1
y = (x +1)^2 + 4

The vertex is at (-1,4)

Step Three
Find the roots. Use the quadratic equation. Note that the graph shows us that the equation never crosses or touches the x axis. The roots are complex.


`\text{x = }\frac{ -b \pm \sqrt{b^(2) - 4ac } }{2a}`

a = 1
b = 2
c = 5


`\text{x = }\frac{ -2 \pm \sqrt{2^(2) - 4*1*5 } }{2}`

`\text{x = }( -2 \pm √(4 - 20 ) )/(2)`

`\text{x = }( -2 \pm √(-16 ) )/(2)`

`\text{x = }( -2 \pm 4i )/(2)`
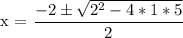
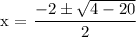
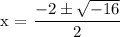
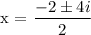
x = -1 +/- 2i

x1 = -1 + 2i
x2 = -1 - 2i And we are done.