Because this is a positive parabola, it opens upwards, like a cup, and the vertex dictates what the minimum value of the function is. In order to determine the vertex, I recommend completing the square. Do that by first setting the function equal to 0 and then moving the 9 to the other side by subtraction. So far:
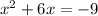
. Now, to complete the square, take half the linear term, square it, and add that number to both sides. Our linear term is 6. Half of 6 is 3 and 3 squared is 9. So add 9 to both sides.
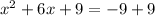
. The right side reduces to 0, and the left side simplifies to the perfect square binomial we created while completing this process.
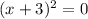
. Move the 0 back over and the vertex is clear now. It is (-3, 0). Therefore, 0 is the minimum point on your graph. The first choice above is the one you want.