WXYZ is a rhombus with vertices W(0,4b), X(2a,0), Y(0,-4), Z(-2,0). You can see thap points W and Y lie on the y-axis and points X and Z lie on the x-axis. Then the centre of the rhombus is origin, thus W and Y are symmetric about the origin. Then b=1 and point W has coordinates (0,4). Similarly points X and Z are symmetric about the origin and a=1, hence X(2,0).
Let KLMN be middlepoints of segments WX, XY, YZ, ZW, respectively. Then
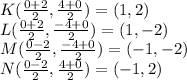
.
Now find the vectors
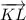
,
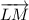
,
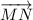
and
:
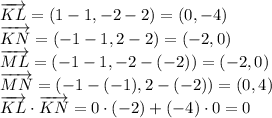
that means that

.
Similarly,

,

,

.
You prove that KLMN is a recctangle.