Question

Would someone mind helping me find the exact value of the expression?

Thank you!!

Answer 1

This is quite a doozy so pay attention. This follows the difference of the trig function cosine where the pattern is
`cos \alpha cos \beta -sin \alpha sin \beta`. We are going to let
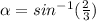
`\alpha =sin ^(-1) ( (2)/(3))` and
`\beta =2sin ^(-1)(- (1)/(3))`. So, following that pattern we can rewrite as
`cos(sin ^(-1)( (2)/(3)))cos(2sin ^(-1)(- (1)/(3)))-sin(sin ^(-1)( (2)/(3)))sin(2sin ^(-1) (- (1)/(3)))`. For inverse sin of 2/3...inverse sin exists in QI and Q!V, but since our y is positive in QI only, that's where our angle is. Sin in opposite over hypotenuse, so we need to find the missing side, the side adjacent to the angle. Using Pythagorean's Theorem, we find that the missing side is
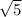
`√(5)`. Therefore, the cos of the angle is
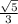
`( √(5) )/(3)`. For
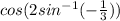
`cos(2sin ^(-1)(- (1)/(3)))`, use the fact that
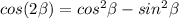
`cos(2 \beta )=cos^2 \beta -sin^2 \beta` where
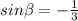
`sin \beta =- (1)/(3)`. Since we are squaring oth sin and cos, it doesn't matter is we are in QIII or QIV so let's just put it in QIV. Side opposite is -1 and hypotenuse is 3, so missing side by Pythagorean's Theroem is
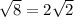
`√(8)=2 √(2)`. Therefore,
`cos(2 \beta )=( (2 √(2) )/(3))^2-(- (1)/(3))^2` which is
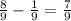
`(8)/(9)- (1)/(9)= (7)/(9)`. Now, since sin and inverse sin undo each other, sin of the inverse sin of 2/3 is 2/3. One more to go...For
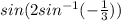
`sin(2sin ^(-1)(- (1)/(3)))`, use
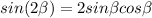
`sin(2 \beta )=2sin \beta cos \beta` where
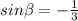
`sin \beta =- (1)/(3)`. Go back to QIV where we had the anlge for cos(2beta) and see that the cosine here is
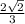
`(2 √(2) )/(3)` and sin here is -1/3. Therefore,
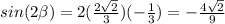
`sin(2 \beta )=2( (2 √(2) )/(3))(- (1)/(3))=- (4 √(2) )/(9)`. Now we are ready to fill in our original difference of cosines formula using all the values we found above:
`( ( √(5) )/(3))( (7)/(9))-( (2)/(3))(- (4 √(2) )/(9))`, which when you do all the simplfying, gives you
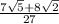
`(7 √(5)+8 √(2) )/(27)`, the last choice listed above. Phew!!!!! told you it was a doozy!