Question

∠ADB and ∠BDC represent a linear pair because points A, D, and C lie on a straight line. Calculate the sum of m∠ADB and m∠BDC. Then move point B around and see how the angles change. What happens to the sum of m∠ADB and m∠BDC as you move point B around?

Answer 1

The sum of m∠ADB and m∠BDC remains the same: m∠ADB + m∠BDC = 180°.

Explanation:

Answer 2

If points A, D and C lie on a straight line, then angles ∠ADB and ∠BDC are supplementary angles and

`m\angle ADB+m\angle BDC=180^(\circ)`.
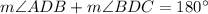
1. If you move point B right from the initial position, then m∠ADB increases and m∠BDC decreases, but
`m\angle ADB+m\angle BDC=180^(\circ)`.
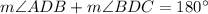
2. If you move point B left from the initial position, then m∠ADB decreases and m∠BDC increases, but
`m\angle ADB+m\angle BDC=180^(\circ)`.
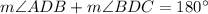
3. When point B lie on the line ADC, then:
a. Point B lies on the right hand from point D:
`m\angle ADB=180^(\circ) \\m\angle BDC=0^(\circ)`;
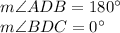
b. Point B lies on the left hand from point D:
`m\angle ADB=0^(\circ) \\m\angle BDC=180^(\circ)`.
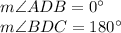
4. When point B is reflected about the line ADC situation is the same as in parts 1 and 2.

Conclusion: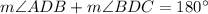
`m\angle ADB+m\angle BDC=180^(\circ)`.