Question

Q1) Find the limit of the function by using direct substitution.:

limit as x approaches quantity pi divided by two of quantity three times e to the x times cosine of x.

Q2)Find the limit of the function by using direct substitution:
limit as x approaches zero of quantity x squared minus one.

Q3)Find the limit of the function algebraically:
limit as x approaches zero of quantity x squared plus three divided by x to the fourth power.

PLEASEEEE answer ASAP thank u SO much! this is super important!

Answer 1

Q1)
For the first question, the function is
f(x)=3eˣ * cos(x)
Now,

`\lim_{x \to \\( \pi )/(2) } 3e^x cos(x)`
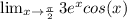
By direct substitution of π/2,
we get,
=
`3e^ ( \pi )/(2) cos( ( \pi )/(2) )` , as cos(π/2)=0
= 0

Q2)
For the second question, the function is
f(x)= x²-1
Now,

`\lim_(x\to \ 0) x^(2) -1`
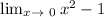
By direct substitution,
the square term will be zero and the answer is -1
= 0 -1
=-1
Q3)
For the third question, the function is
f(x)=x²+3/x⁴
Now,

=
`\lim_(x\to \ 0) x^(2) +(3)/( x^4 )`
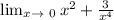
Now, by using the property of limit separate the limit with both x² and 3/x⁴
the x² term will be zero and the second term will approach infinity.
=
`\lim_(x\to \ 0) x^(2) +\lim_(x\to \ 0) (3)/( x^4 )`
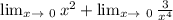= infinity is the correct answer.