Question

Complete the square to rewrite y = x^2 – 6x + 5 in vertex form. Then state whether the vertex is a maximum or a minimum and give its coordinates.

A. Minimum at (–3, –4)
B. Maximum at (3, –4)
C. Minimum at (3, –4)
D. Maximum at (–3, –4)

Answer 1

The first thing to do is to set this equal to zero, then move the constant over to the other side of the equals sign so we only have the x terms to worry about.
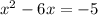
`x^(2) -6x=-5`. Now we're ready to complete the square. We take half the linear term, square it, and add it in to both sides. Our linear term is -6x. Half of 6 is 3, and 3 squared is 9, so we add 9 to both sides:
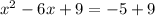
`x^(2) -6x+9=-5+9`. Now we will do the math on the right to get 4, and on the left we will express the perfect square binomial we created while completing this process.
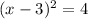
`(x-3)^2=4`. Now we can move the constant back over by subtraction to get
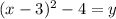
`(x-3)^2-4=y`. Now we can see that the vertex is (3, -4). Since this is a positive parabola, it opens upwards, like a cup, which means that the lowest part of the parabola, the vertex, is sitting at the bottom, or at a minimum value. So our answer is C