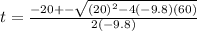Answer:
option C
Explanation:
The projectile motion of an object can be modeled using h(t) = gt2 + v0t + h0, where g is the acceleration due to gravity. The acceleration due to gravity is –9.8 m/s2
An object is launched at an initial velocity of 20 meters per second and an initial height of 60 meters.
g= -9.8, v0 = 20 and h0 = 60
So the equation becomes
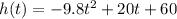
When the object hit the ground the height =0 so we replace h(t)=0
Apply quadratic formula
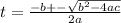
a= -9.8 , b=20 and c= 60