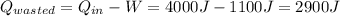Question

An automobile engine takes in 4000 j of heat and performs 1100 j of mechanical work in each cycle. (a) calculate the engine's efficiency. (b) how much heat is "wasted" in each cycle?

Answer 1

(a) The efficiency of an engine is defined as the ratio between the work done by the engine and the heat it takes in:

`\eta= (W)/(Q_(in))`
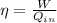
The engine in this problem does a work of
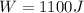
`W=1100 J` and it takes in
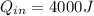
`Q_(in)=4000 J` of heat, therefore its efficiency is

`\eta= (1100 J)/(4000 J)=0.275 = 27.5 \%`

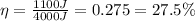
(b) The heat taken by the machine is 4000 J; of this amount of heat, only 1100 J are converted into useful work. This means that the rest of the heat is wasted. Therefore, the wasted heat is the difference between the heat in input and the work done by the engine:

`Q_(wasted)=Q_(in)-W=4000 J-1100 J=2900 J`