Question

Andrea works at a zoo that just purchased a new lion and two parakeets. Andrea needs to change a section of the lion's habitat from sand to grass. She also needs to fill up the parakeets' food dispenser. Her boss told her that the length of the grassy area for the lion must be 3 feet greater than its width and that the food dispenser for the parakeets must be filled up completely. To give the lion enough grass, the area of the grass must be at least 8 times greater than the radius of the parakeets' food dispenser.

The food dispenser for the parakeets is cylindrical in shape and 4 feet tall. It is exactly half-way full. The cost of the parakeets' food is $0.49 times the length of the radius for every foot of height of food missing from the dispenser. Also, the landscaping crew said they could put the grass in the lion's habitat for $2.84 per square foot of grass. Andrea cannot spend more than $751.00 on both projects.

If x represents the width of the grassy area and y represents the radius of the parakeets' food dispenser, then which of the following systems of inequalities can be used to determine the length and width of the grassy area and the radius of the food dispenser?

Answer 1

its A for plato users

Answer 2

The correct answer is D: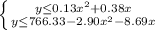

`\left \{ {{y \leq 0.13 x^(2) + 0.38 x } \atop {y \leq 766.33 - 2.90x^(2) - 8.69x}} \right.`

Given:
x = width of the grass
y = radius of the dispenser

Let's see each statement of the question and write it in Mathematical language:
- "the length of the grassy area for the lion must be 3 feet greater than its width" can be written as:
l = x + 3

- "the area of the grass must be at least 8 times greater than the radius of the parakeets' food dispenser" can be written as:
A ≥ 8 · y

Considering that the area of a rectangle is given by:
A = l · w
= (x + 3) · x

We can write the first inequality:
(x + 3) · x ≥ 8 · y
x² + 3x ≥ 8y

and solving for y:
y ≤ 0.13x² + 0.38x (rounded to two decimal digits)

Let's see the other statements:

- "The food dispenser for the parakeets is … 4 feet tall. It is exactly half-way full" means that the empty height of the dispenser is:
h = 4 : 2 = 2 ft

- "The cost of the parakeets' food is $0.49 times the length of the radius for every foot of height of food missing from the dispenser" can be written as:
P = 0.49 · y · h
= 0.98y

- "They could put the grass in the lion's habitat for $2.84 per square foot of grass" can be written as:
G = 2.84 · A
= 2.84 · (x² + 3x)
= 2.84x² + 8.52x

- "Andrea cannot spend more than $751.00 on both projects" can be written as:
P + G ≤ 751.00

We can now write the second inequality:
(0.98y) + (2.84x² + 8.52x) ≤ 751.00

Solving for y:
0.98y + 2.84x² + 8.52x ≤ 751.00
0.98y ≤ 751.00 - 2.84x² - 8.52x
y ≤ 766.33 - 2.90x² - 8.69x

Hence, the option involving the two inequalities is option D.