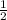Notice that the graph is decreasing as x increases, showing exponential decay. An exponential decay graph is in the form
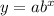
, where a is just multiplying
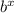
and
b < 1. That means
the value of b we are looking for is less than 1. This isn't crucial information, but it's nice to know!
Also remember the
negative exponent rule says that when a base has a negative exponent, flip the base onto the other side of the fraction to make it into a positive exponent. For example,
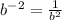
.
Back to the ProblemLet's pick out an easy value on the graph. I went with (-1, 2). Since we know the equation is
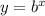
, plug the coordinate in and solve for b:
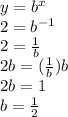
-----
Answer:b =