Question

The slope of the tangent line to a curve at any point (x, y) on the curve is x divided by y. What is the equation of the curve if (2, 1) is a point on the curve?

a) x + y = 3
b) x^2 - y^2 = 3
c) x^2 + y^2 = 3
d) xy = 3

Answer 1

Option b -
`x^2-y^2=3`

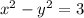
Explanation:

Given : The slope of the tangent line to a curve at any point (x, y) on the curve is x divided by y.

To find : What is the equation of the curve if (2, 1) is a point on the curve?

Solution :

We know that,

The slope of the tangent line is the derivative.

So,
`(dy)/(dx)=(x)/(y)`

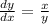
or
`yy'=x`

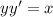
Subtract yy' on both side of the equation,

`x-yy'=0`

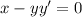
Now, Integrating both side of the equation but keeping concept of implicit differentiation,

`((1)/(2))x^2-((1)/(2))y^2=c`

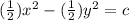
Where, c is the constant.

Solving the equation,

`((1)/(2))(x^2-y^2)=c`

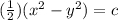
Substitute x=2 and y=1 to find c,

`((1)/(2))(2^2-1^2)=c`

`((1)/(2))(3)=c`

`c=(3)/(2)`

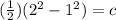
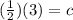
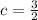
Substitute c back in the equation,

`((1)/(2))(x^2-y^2)=(3)/(2)`

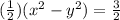
Solving,

`x^2-y^2=3`

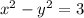
Therefore, The required equation is
`x^2-y^2=3`

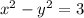
So, Option b is correct.

Answer 2

The curve must have a positive slope in the first quadrant. The only choice that does is
b) x^2 - y^2 = 3