You need a system of 3 equations to solve for the 3 unknowns in our parabola, standard form of
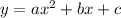
. Since the second point there has an x of 0, we'll start there to make it easy. In this point, x = 0 and y = -4.
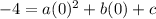
. That gives us our first value...c = -4. Let's do the first equation now the same way, but this time we have a c value to sub in:

and
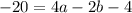
which simplifies to
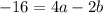
. We'll use that in a bit. Let's do the third point now the same way.
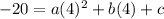
and
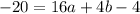
which simplifies to
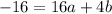
. Now we have a new system of equations. We need to solve for a and b. Let's multiply the 2nd equation by -4 to get rid of the a terms. Doing that we have
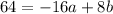
and we will add that to
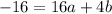
. The a terms cancel each other out leaving us with 48=12b and b = 4. Now we'll sub that b into one of the equations in terms of a and b and solve for a. -16 = 16a + 4(4) and -16=16a+16. Subtracting 16 from both sides and we have -32=16a and a = -2. Here's what we have for our values now: a = -2 b = 4, c = -4. So the quadratic in standard form is
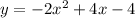
. And you're done!