Question

What is the answer to this question?

Answer 1

Lets start by factoring the 216 into its smaller parts.

`\sqrt[3]{2 * 2 * 2 * 3 * 3 * 3}`
From here, we can separate the three 2s and the three 3s into two separate radicals.

`\sqrt[3]{2*2*2} * \sqrt[3]{3*3*3}`
Since we have three copies of the same number in each, the answer to the cube root is the number we have the copies of.

`\sqrt[3]{2*2*2} * \sqrt[3]{3*3*3} = 2 * 3`
Finally, we just need to multiply out what remains to find the solution.

`2*3 = 6`
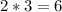
So, the final answer is 6.