Question

α, β, γ are the zeroes of the polynomial x^3 + px^2 + qx + 2 such that α+ β + 1 = 0. Find the value of 2p + q + 5.

Answer 1

Hi there!

α, β, γ are the zeroes of the polynomial x³ + px² + qx + 2

Then,

• α + β + γ = - p ---(i)

• αβ + βγ + γα = q. ---(ii)

• αβγ = - 2. ---(iii)

We're Given :-

αβ + 1 = 0 Or αβ = - 1

Substitute " αβ = - 1 " in eqn. (iii) :-

(- 1) γ = - 2

γ =
`\frac {- 2}{- 1}`

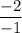
γ = 2

Now. Accr'ding to the question :-

2p + q + 5 = - 2 (α + β + γ) + (αβ + βγ + γα) + 5

= - 2 (α + β + γ) + (αβ + [ γ (β + α) ] + 5

= - 2 (α + β + 2) + [ - 1 + 2 ( α + β ) ] + 5

= - 2α - 2β - 4 - 1 + 2α + 2β + 5

= 5 - 5

= 0

∴ 2p + q + 5 = 0

~ Hope it helps!