Question

write the equation of the transformed graph of sine with period pi that has been shifted vertically up 3 unit and has an amplitude of 3/4

Answer 1

(3/4)sin(2x)+3 is the transformed equation

Answer 2

`f(x)=(3)/(4)\sin (2x)+3`

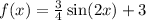
Explanation:

We have the function,
`f(x)=\sin x`

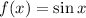
It is required to form a function with period
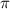`\pi`, shifted vertically 3 units upwards and having amplitude =
`(3)/(4)`

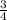
Now, as we know, 'If a function f(x) has the period P, then f(bx) will have period
`(P)/(|b|)`'.

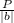Since, the new function need to have period
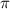`\pi`, that is the value
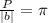`(P)/(|b|)=\pi` i.e.
`(2\pi)/(|b|)=\pi`.

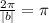So, b= 2 implies the new function is
`f(x)=\sin (2x)`

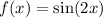
Further, as the function need to be vertically shifted 3 units upwards, we get the new function,
`f(x)=\sin (2x)+3`.

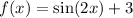Finally, the amplitude of the function must be
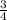`(3)/(4)`, this means that the maximum and minimum value of the function is
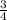`(3)/(4)` and
`(-3)/(4)`.

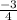This gives us the transformed final function is
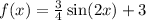`f(x)=(3)/(4)\sin (2x)+3`.